矩阵的逆 C 语言 算法二

一.初等变换法

如果矩阵A和B互逆，则AB=BA=E。由条件AB=BA以及矩阵乘法的定义可知，矩阵A和B都是方阵。再由条件AB=E以及定理“两个矩阵的乘积的行列式等于这两个矩阵的行列式的乘积”可知，这两个矩阵的行列式都不为0。也就是说，这两个矩阵的秩等于它们的级数（或称为阶，也就是说，A与B都是方阵，且rank(A) = rank(B) = n）。换句话说，这两个矩阵可以只经由初等行变换，或者只经由初等列变换，变为单位矩阵。

因为对矩阵A施以初等行变换（初等列变换）就相当于在A的左边（右边）乘以相应的初等矩阵，所以我们可以同时对A和E施以相同的初等行变换（初等列变换）。这样，当矩阵A被变为E时，E就被变为A的逆阵B。

二.算法

#include <stdio.h>
#include <stdlib.h>

void main()
{
    int i,j,res;
    int dimension;
    double **array,**deterArray, **result, *temp;

    double primaryRowChange(int s, int n, double **array);
    void primaryRowChange2(int s, int n, double **array);
    void printfDouble2Dimension(int s, int n, double **array);

    printf("请输入方阵的阶数N:");
    scanf("%d",&dimension);

    array=(double**)malloc(dimension*sizeof(double*));
    deterArray=(double**)malloc(dimension*sizeof(double*));
    result =(double**)malloc(dimension*sizeof(double*));

    //循环输入方阵
    for(i=0;i<dimension;i++)
    {
        temp=(double*)malloc(dimension*sizeof(double));
        deterArray[i]=(double*)malloc(2*dimension*sizeof(double));
        result[i]=(double*)malloc(dimension*sizeof(double));

        printf("请输入方阵的第%d行:",i+1);
        for(j=0;j<dimension;j++)
            scanf("%lf",temp+j);
        array[i]=temp;
    }

    for(i=0;i<dimension;i++)
    {
        for(j=0;j<2*dimension;j++)
        {
            if(j<dimension)
            {
                *(*(deterArray+i)+j) = *(*(array+i)+j);
                continue;
            }
            //合并单位矩阵
            if(j-dimension ==i)//对角线为1，其余为0
                *(*(deterArray+i)+j) = 1;
            else 
                *(*(deterArray+i)+j) = 0;
        }
    }

    printf("输入矩阵如下:\n");
    printfDouble2Dimension(dimension,dimension,array);

    printf("合并单位矩阵如下:\n");
    printfDouble2Dimension(dimension,2*dimension,deterArray);

    res = primaryRowChange(dimension,2*dimension,deterArray);
    printf("初等变换之后如下:\n");
    printfDouble2Dimension(dimension,2*dimension,deterArray);

    if(res==0)
    {
        printf("矩阵行列式的值为0，矩阵无逆矩阵.");
    }
    else
    {        
        primaryRowChange2(dimension,2*dimension ,deterArray);

        printf("继续变为单位矩阵之后:\n");
        printfDouble2Dimension(dimension,2*dimension,deterArray);

        for(i=0;i<dimension;i++)
        {
            for(j=dimension;j<2*dimension;j++)
                *(*(result+i)+j-dimension) = *(*(deterArray +i)+j);
        }

        printf("矩阵的逆如下:\n");
        printfDouble2Dimension(dimension,dimension,result);
    }
    system("pause");
}

//初等行变换
double primaryRowChange(int s, int n, double **array)
{
    int i,j,k,ii,kk,flag;
    double temp,result=1;
    for(i=0,j=0;i<s-1;i++,j++)//s行，最外围只需要变换s-1
    {        
        ii=i;
        //如果行的首元为0，向下查找一个不为0的，然后换行
        if(*(*(array+i)+j) == 0)
        {
            flag=0;
            for(k=i+1;k<s;k++)
            {
                if(*(*(array+k)+j)!=0)//第k行与第i行交换
                {
                    for(kk=j;kk<n;kk++)
                    {    
                        temp=*(*(array+k)+kk);
                        *(*(array+k)+kk) = *(*(array+i)+kk);
                        *(*(array+i)+kk) = temp;
                    }            
                    flag =1;
                    break;
                }
            }        
            //判断是交换成功，如果没有成功，则i--
            if(!flag)
            {                
                i--;
                continue;
            }
            i--;
            j--;
            continue;
        }
        for(;ii<s-1;ii++)
        {
            if(*(*(array+ii+1)+j)==0)
                continue;
            temp =-*(*(array+ii+1)+j) / *(*(array+i)+j);
            for(k=j;k<n;k++)
                *(*(array+ii+1)+k) += *(*(array+i)+k) * temp;

        }
    }

    //计算行列式的值 
    for(i=0;i<s;i++)
    {
        result *= *(*(array+i)+j);
    }
    return result;
}

void primaryRowChange2(int s, int n, double **array)
{
    int i,j,k,l;
    double temp;
    for(i=s-1,j=s-1;i>=0;i--,j--)
    {
        if(*(*(array+i)+i)!=1)
        {
            temp = 1 / *(*(array+i)+i);
            for(k=0;k<n;k++)
                *(*(array+i)+k) *= temp;
        }

        for(k=i-1;k>=0;k--)
        {
            if(*(*(array+k)+j) ==0)
                continue;
            temp = - *(*(array+k)+j) / *(*(array+i)+j);

            for(l=0;l<n;l++)
                *(*(array+k)+l) += temp * *(*(array+i)+l);
        }
    }
}


//打印数组
void printfDouble2Dimension(int s, int n, double **array)
{
    //printf("%d,%d",s,n);
    int i,j;
    for(i=0;i<s;i++)
    {
        for(j=0;j<n;j++)
        {
            printf("%6.2lf",*(*(array+i)+j));    
        }
        printf("\n");
    }
}

三.程序截图

1> p211-例2

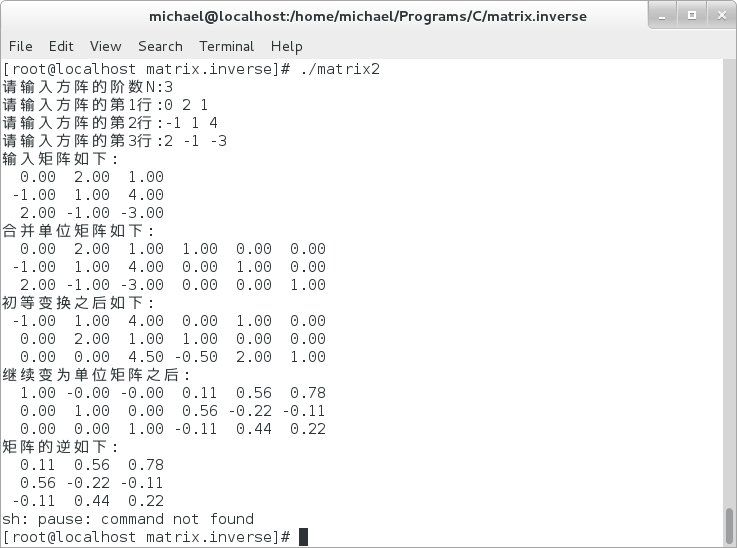
2> 3.4-5.1

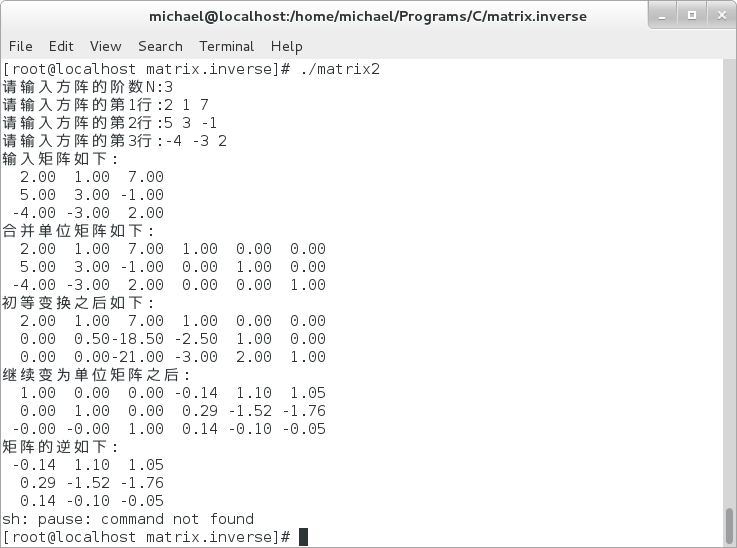
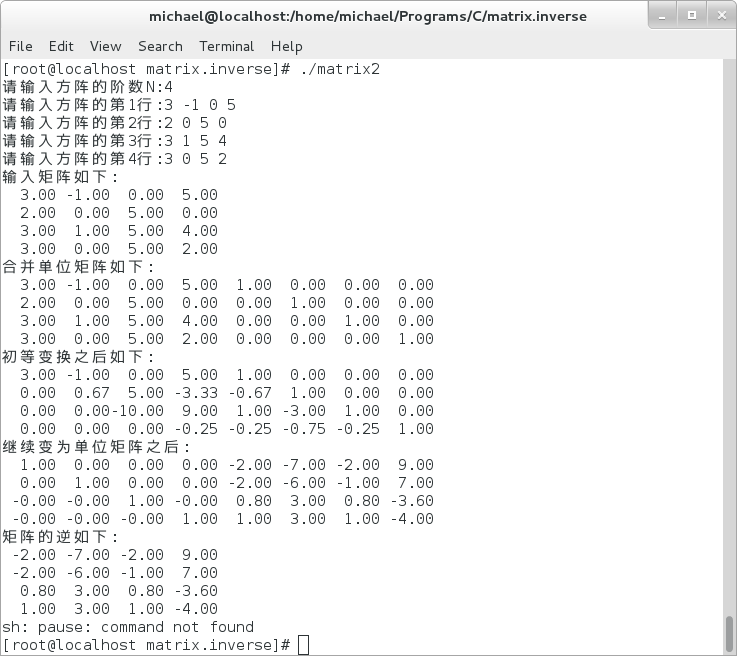
3> 3.4-5.2

评论

Reply